
3.- Vectores
Los vectores son modelos matemáticos.
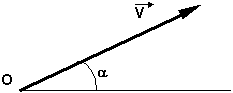
Sea el vector V, representa una cantidad física y se compone de
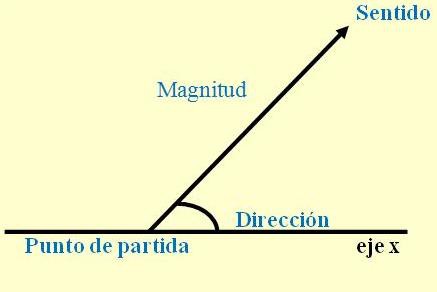
1. Módulo (magnitud): valor numérico y absoluto del mismo, expresa la cantidad que representa el mismo y se le asigna una unidad
2. Dirección: recta de acción que según el sistema de referencia posee una inclinación α (alfa)
3. Sentido: según el sistema de referencia tendrá signo positivo o negativo
4. Origen: punto de aplicación
Se distingue entre magnitudes escalares y magnitudes vectoriales. Se llaman magnitudes escalares aquellas en que sólo influye su tamaño. Por el contrario, se consideran magnitudes vectoriales aquellas en las que, de alguna manera, influyen la dirección y el sentido en que se aplican.
Ejemplos de magnitudes escalares son la masa de un cuerpo, la temperatura y el volumen. Pero cuando se plantea un movimiento no basta con decir cuánto se ha desplazado el móvil, sino que es preciso decir también en qué dirección y sentido ha tenido lugar el movimiento.
Vectores fijos
Un vector fijo del plano es un segmento cuyos extremos están dados en un cierto orden. Se representa por AB, siendo los extremos A y B. Los puntos en los que empieza y termina un vector se llaman origen y extremo, respectivamente.
Módulo, dirección y sentido de un vector fijo
En un vector fijo se llama módulo del mismo a la longitud del segmento que lo define. El módulo de un vector fijo AB se representa por |AB| y se leerá «módulo de AB ».
Se dice que un vector fijo tiene la misma dirección que otro si los segmentos que los definen pertenecen a rectas paralelas. Dados dos vectores fijos AB y CD del plano que tengan la misma dirección, se dice que tienen el mismo sentido si los segmentos AD y BC (los segmentos que unen el origen de cada uno con el extremo del otro) tienen un punto en común. En otro caso se dice que los dos vectores tienen sentido contrario o sentido opuesto.
Se dice que dos vectores son equipolentes si tienen el mismo módulo, la misma dirección y el mismo sentido.
Suma de vectores
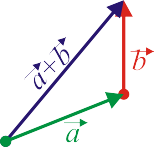
Dados dos vectores libres del plano a y b, se define su suma como el vector libre construido así:
- Se elige un punto arbitrario del plano, O.
- Con origen en O se busca un representante del vector a. Se llamará P a su extremo.
- Con origen en P se busca el vector PQ, representante de b.
- El vector suma a + b viene representado por el vector fijo, OQ (se une el origen del representante de a con el extremo del representante de b).
Propiedades de la suma de vectores
Conmutativa: Dados dos vectores del plano a y b, a + b = b + a.
Asociativa: Dados tres vectores a y b y c del plano, (a + b) + c = a + ( b + c).
Elemento neutro: Dado a, un vector cualquiera del plano, a + 0 = 0 + a = a.
